Erläuterungen zur Strecken- /Flächenreduktion

Auf Grund der Projektion der Koordinaten in die Ebene müssen die Strecken reduziert werden. Bei UTM-Abbildungen wird der Maßstab mit 0,9996 angegeben, wodurch Strecken in der Ebene geringer sind.

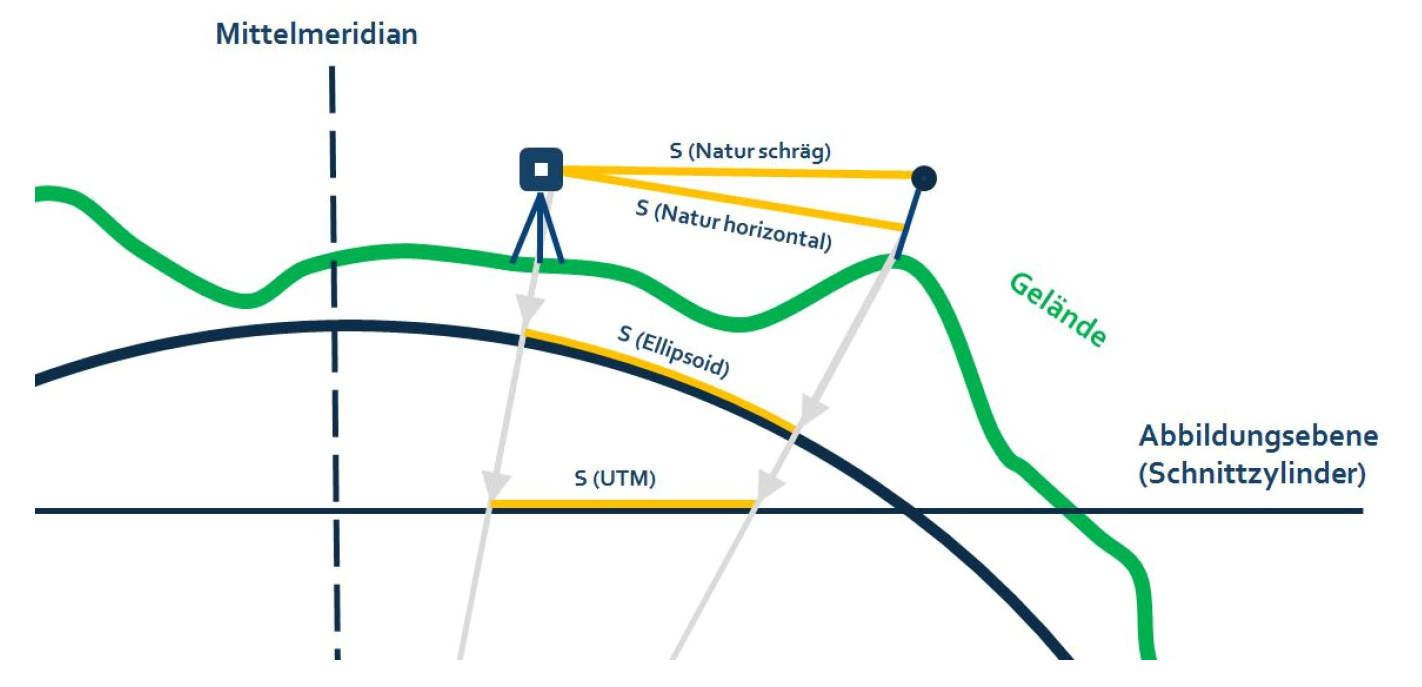
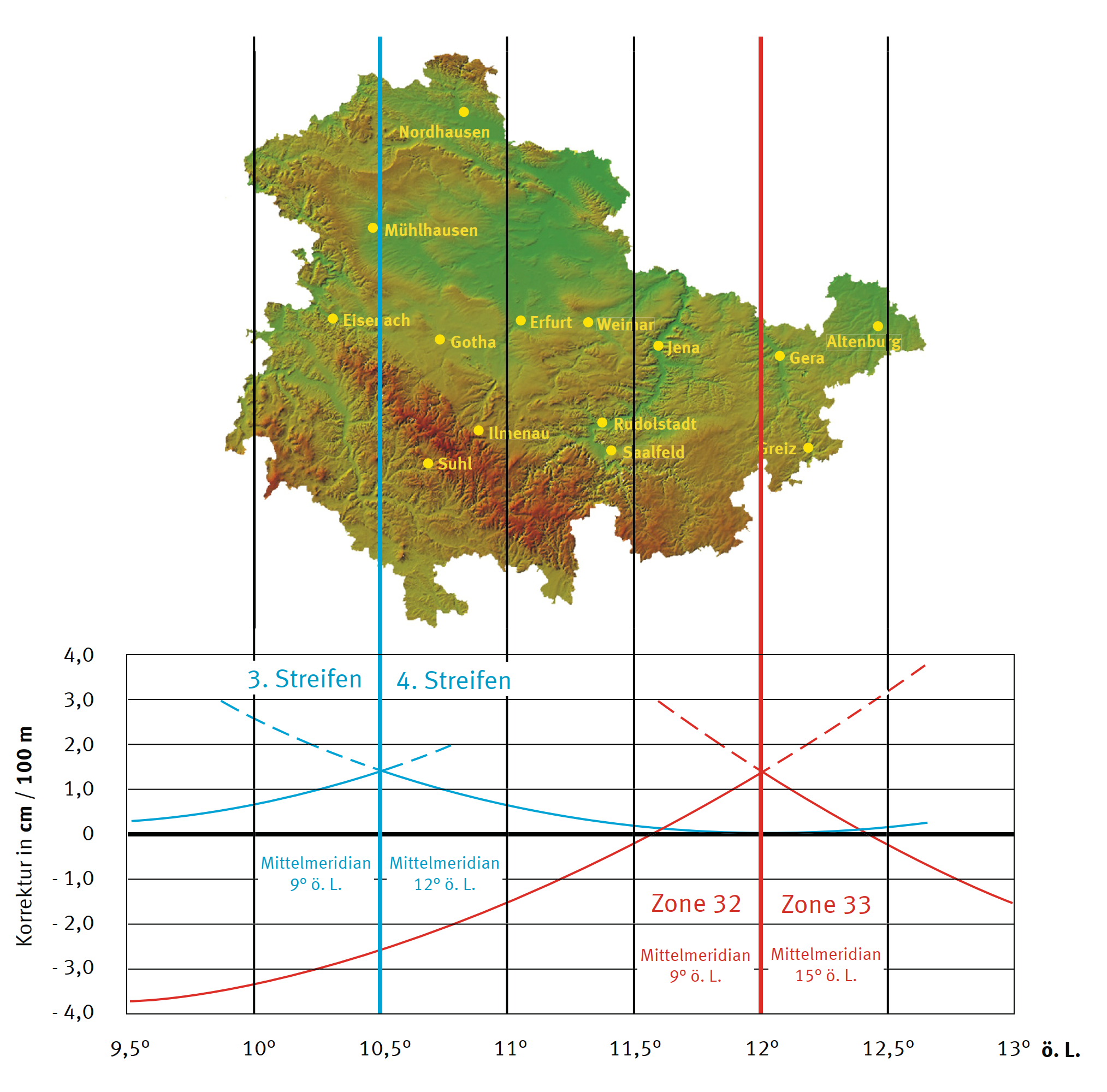
Bei der Streckenreduktion gibt es einen höhenabhängigen Term und einen Term der Abhängig von der Entfernung zum Mittelmerdian ist. Die Abbildung zeigt den Unterschied der Streckenreduktion zwischen der Gauß-Krüger und er der UTM-Abbildung.

Die Formel für die Reduktion lautet:

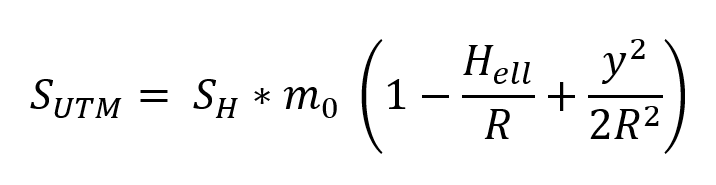
S_H    Horizontalstrecke im Messgebiet
H_ell    mittlere Höhe von SH über Ellipsoid (Höhe NHN + 45m)
R    mittlerer Erdradius 6383 km bzw. 6,383*10+6 m
y    Abstand vom Mittelmeridian [km] (y = ((E-32500000)/1000)/m0)
m₀    Abbildungsmaßstab des Mittelmeridians 0,9996

Quelle: ThürVV-LiKa Anlage 4       

Verfahrensweise:

Eine im Gelände gemessenen schräge Strecke wird mit dem Höhenunterschied zwischen den beiden Punkten waagerecht gerechnet. Die dann horizontal (gemessene) Strecke wird im ersten Schritt von der Geländehöhe auf das Ellipsoid reduziert. Dazu wird die Höhe über dem Ellipsoid bzw. näherungsweise die Normalhöhe + 46m (für ETRS89 in Thüringen) benötigt. Die Strecke wird durch diese Reduktion kürzer. Im zweiten Schritt findet die Verebnung vom Ellipsoid auf die Koordinatenebene statt. Dafür wird der mittlere Abstand der Punkte zum Mittelmeridian benötigt.

Genauigkeit:

Die Genauigkeit der Formel liegt bei < 10 ppm (1 cm auf 1 km). Dafür muss die Höhe auf 10m genau angegeben werden.
Die Anzahl der Kommastellen bei der Ergebnisausgabe wird aus der der Eingabe abgeleitet bzw. auf 10 ppm begrenzt. Strecken über 150 km werden nicht gerechnet.

Flächenreduktion:

Zwischen aufeinanderfolgenden Punkten werden die Strecken und die verschiedenen Reduktionsstände gerechnet.
Eine Flächenausgabe gibt es nur, wenn der erste Punkt mit dem letzten identisch ist (Fläche geschlossen) und mindestens ein Dreieck vorliegt. Geprüft werden Punktnummer, Koordinaten und die Höhe. Dabei sollten sich die Strecken nicht schneiden, da sonst die Berechnung ein falsches Ergebnis liefert.
Eine schräge Fläche gibt es nur im Dreiecksfall. Es wird dafür angenommen, dass die Fläche im schrägen Dreieck eben ist. Bei Flächen mit mehr als 3 Eckpunkten kann keine sinnvolle Aussage über den Höhenverlauf in der Fläche erraten werden.